前言
卷积神经网络(CNN)是一种著名的深度学习模型,其名称的由来是因为卷积运算被引入到了这种模型中,CNN可以归类为多层前馈神经网络模型(BP神经网络模型)在计算机视觉领域中得到了非常广泛的应用,例如图像分类、目标检测及跟踪等。下面,将详细介绍CNN的基本原理。
why CNN
CNN的输入是二维模型,所以利于处理图像视频的高维数据,同时由于其不用手动提取特征,使得在实际应用中可以大展身手,不过由于模型中所需参数极多,对计算机的计算力要求较高,加上训练模型所需要的数据量很大,所以在上世纪九十年代提出之后,基本没有得到大规模应用。随着大数据时代的到来,在高性能计算平台上用大规模的数据集训练复杂模型,成为了可能,正是在这种背景下,卷积神经网络开始蓬勃发展
CNN基本结构
卷积神经网络顾名思义就是:卷积+神经网络,前面的博客中我已经详细介绍了图像卷积和BP神经网络,所以阅读这篇博客的读者,我就默认你们已经阅读过了前面的内容,还木有了解的小伙伴赶快点击上面链接。
先来看一下CNN的基本结构: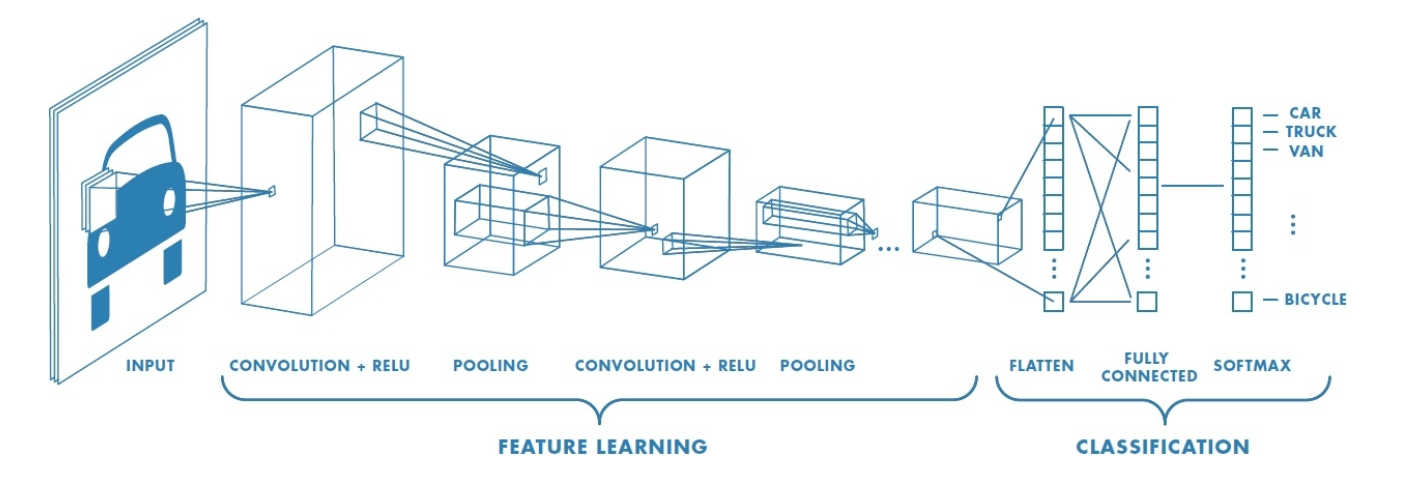
主要有卷积层,池化层,全连接层,输出层,另外还涉及两个函数,激活函数和softmax函数,下面将一一进行介绍。
卷积层
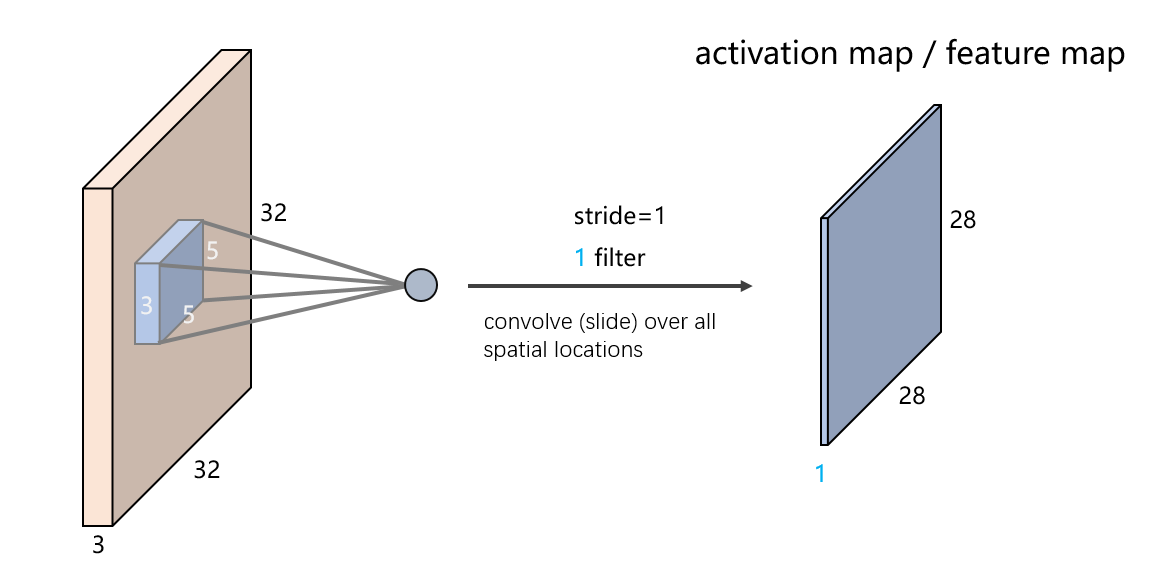
我们知道传统的机器学习方法中,我们要手动进行特征选择和特征提取,而在CNN中是不需要我们提取特征,CNN会自动进行特征提取,那么CNN是怎么做到的呢,对了,特征提取的工作就由卷积层负责。我们在图像卷积那里提到,卷积其实就是滤波,滤波和神经网络又有什么关系呢?我们设想一下,如要识别图像中某种特定曲线,是不是就要用滤波器将其他曲线信号给抑制,让这种曲线经过滤波器时有很高的输出,这其实就是卷积层的特征提取过程了(详细过程见图像的卷积)这种滤波器,我们称为卷积核,一个卷积核只负责提取一种特征,卷积层一般又多个卷积核组成。 其过程动图如下:
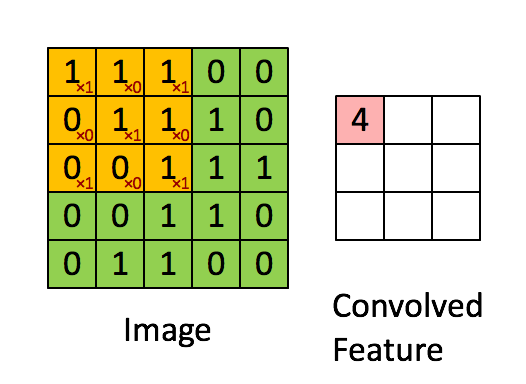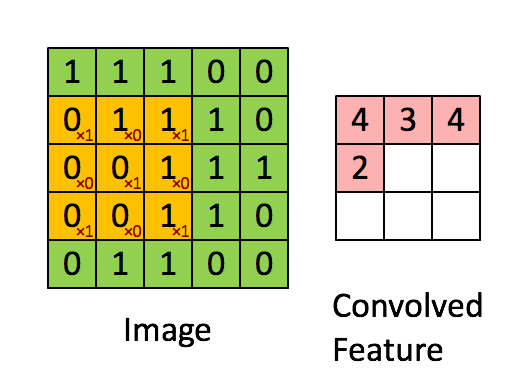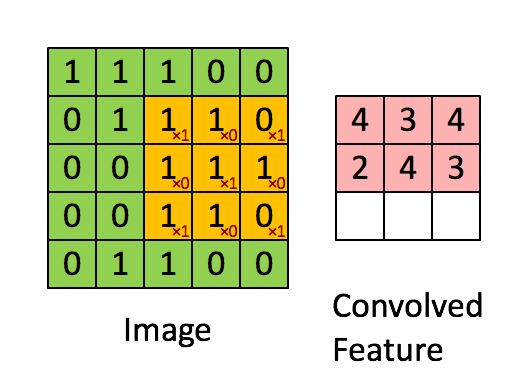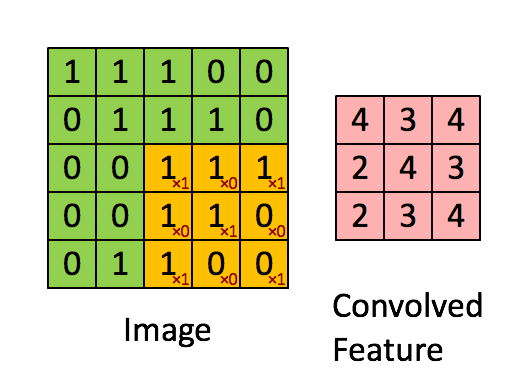

对于卷积层,其输入是原始图像,输出是三个通道的特征图,原始图像和特征图维数的关系如下:
(W−F+2P)/S+1
其中W:输入单元的大小(宽或高)
F:卷积核的大小
S:步幅(stride)
P:补零(zero-padding)的数量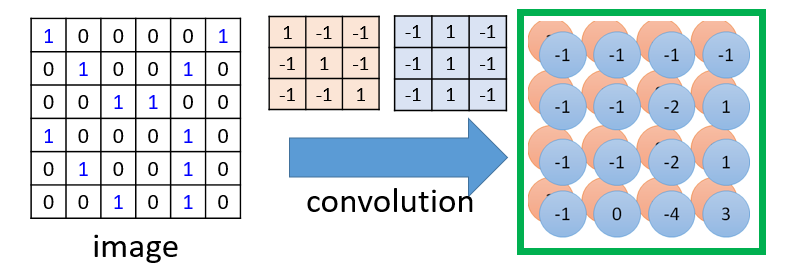
池化层
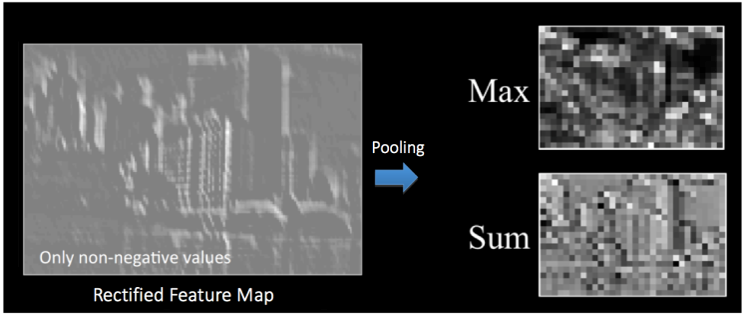
池化层的作用用一句话概括就是:采样降维。试想一下,如果用传统神经网络的全连接方式,对于上面28X28的特征图就需要28^4个参数,这还只是一个通道的一个特征图,显而易见,我们需要先降维。先将特征图划分小区域(一般为2X2小区域),然后用区域内最大值代替此区域,这就是最大池化;或用区域均值代替,这就是均值池化。如下图所示: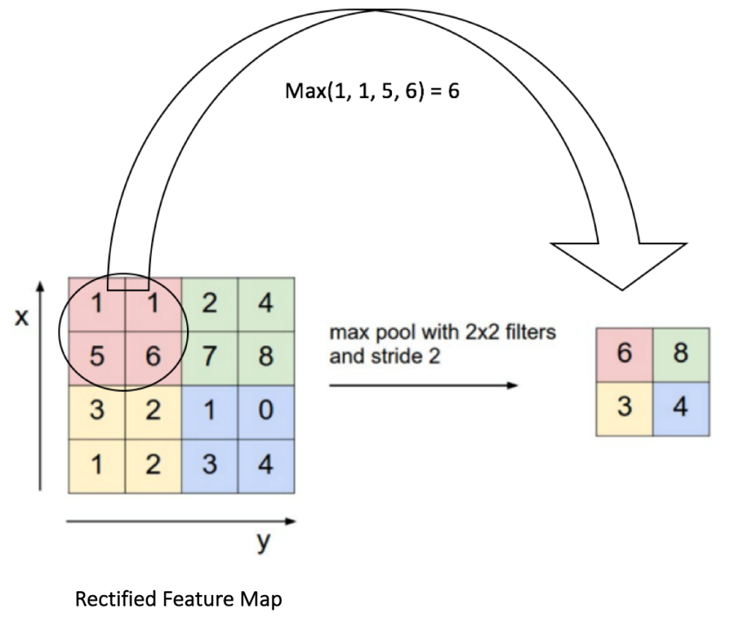
全连接层
在前面,我们提到过,在传统神经网络中,我们使用的就是全连接,在卷积神经网络中,全连接层又有什么用呢?先来看全连接层的结构图: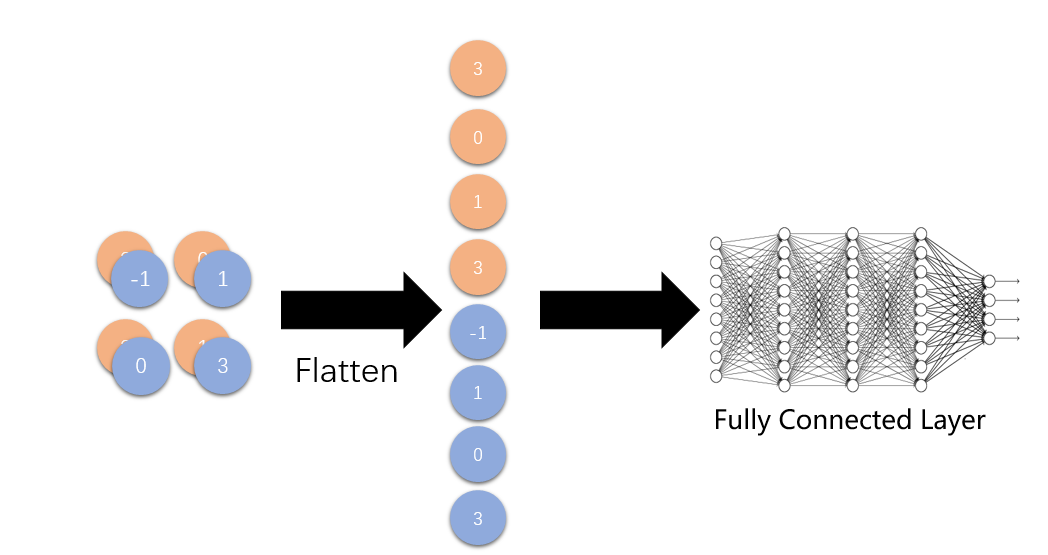
我们可以看到,全连接层其实就是将多维特征图展开成一维,为什么要这么做呢,我们来看下面几张图:


他们都是猫但猫的位置和角度都不同,那么输入矩阵和特征矩阵肯定也是不一样的,但是我们的神经网络还是能识别出来,这就是全连接层做的,全连接层实际上呢识别前面提取到的特征进行组合,也就是说含有一维特征集中只要含有某些特征,就判断成猫,跟它的位置没有关系。
输出层与softmax函数
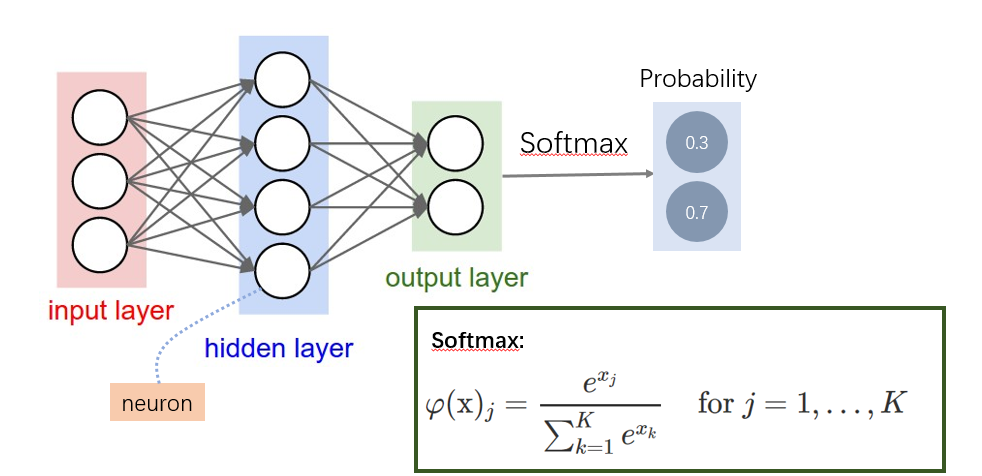
输出层神经元个数是与类别个数相一致的,因为我们的网络最终要依靠输出层的值来判断类别,但是输出层输出数值啊,如何根据数值判断类别呢,答案就是把数值转化成概率,概率大的类别即为神经网络最终的输出,这就是softmax函数的作用啦。
好了,到这里,整个神经网络的基本结构就介绍完了,慢着是不是感觉还缺少点什么,我们的神经网络是不是还是有点简单呢,对了,少了个激活函数啊。
激活函数
在卷积层输出,一般会加上个激活函数,激活函数是用来干什么的呢
一句话,激活函数是用来加入非线性因素的,因为线性模型的表达能力不够。
这是个单层的感知机,显而易见的是,它只能执行线性分类任务,
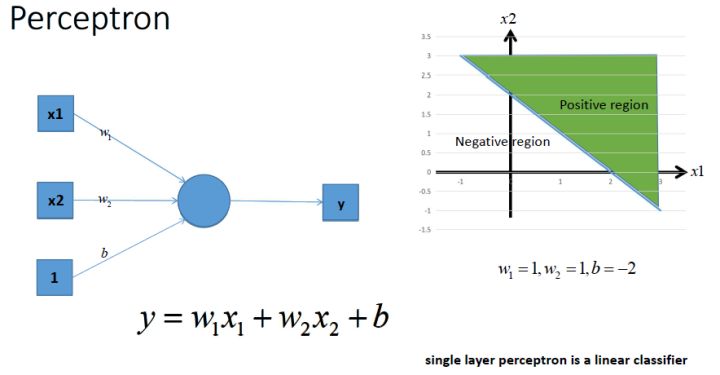
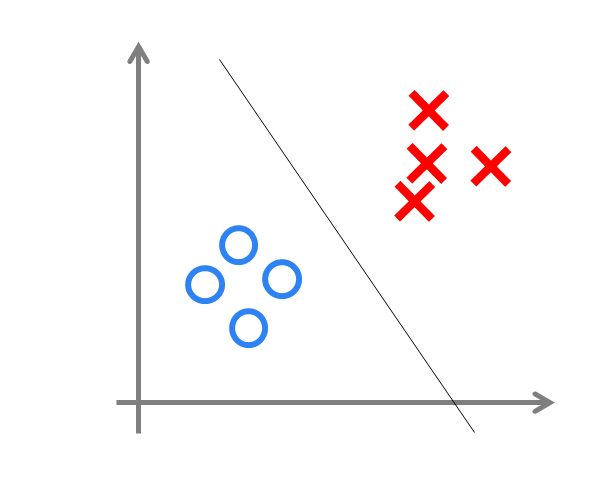
这时候,我们加入激活函数,使其具有非线性分类的能力,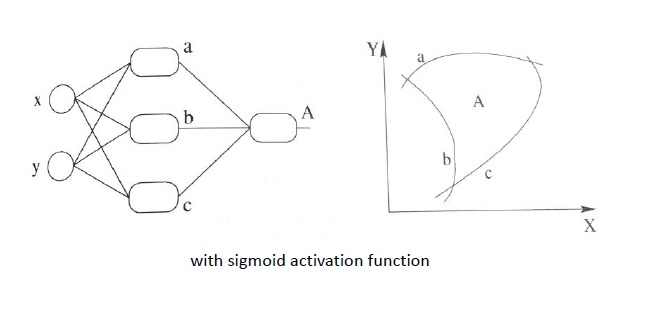
不知道各位看到这里想到了什么,很像SVN里面的核函数对不对,对了,他们的作用是一样的,引入非线性因素。
值得注意的是激活函数一般放在卷积层的输出,主要的激活函数有tanh, sigmoid和reLu等。
模型训练
模型训练其实就是调参,所有参数初始阶段都是随机的,后面根据输出值和目标值之间的差值进行误差反向传播来调整参数值,详细介绍见BP神经网络
小结
以上我们介绍的只是卷积神经网络的基本结构,实际上卷积核数量和其他各层数量,理论上都是可以任意添加的,这个可以根据具体任务来确定。
