图像的卷积

前言

说到卷积，我想大多数人想到的是信号系统里面的卷积还有傅里叶变换，没错图像的卷积和信号系统里面的卷积非常类似，只不过前者是空间域上的，后者是时间域上的。看到卷积傅里叶，大家就本能的头疼对不对，没关系，本文将尽量摈弃复杂的数学公式，力求通俗易懂的解释图像的卷积。

---

卷积介绍

卷积定义

我们先来看看信号系统里面的卷积：


其实质就是延迟加权求和，如下图所示：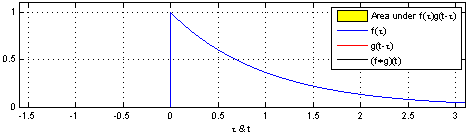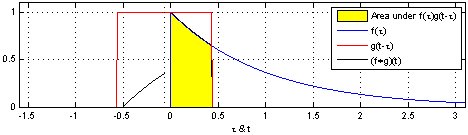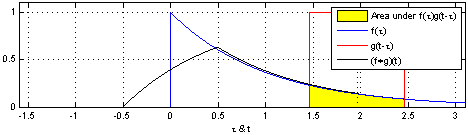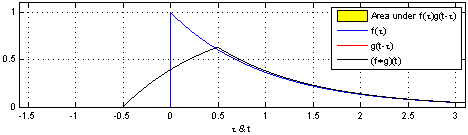

我们可以看到，这是在时间域上的平移，而我们图像则是空间域上的卷积。 用一个卷积核去扫图像，图像对应部分和卷积核相乘后的矩阵求和作为新的值填充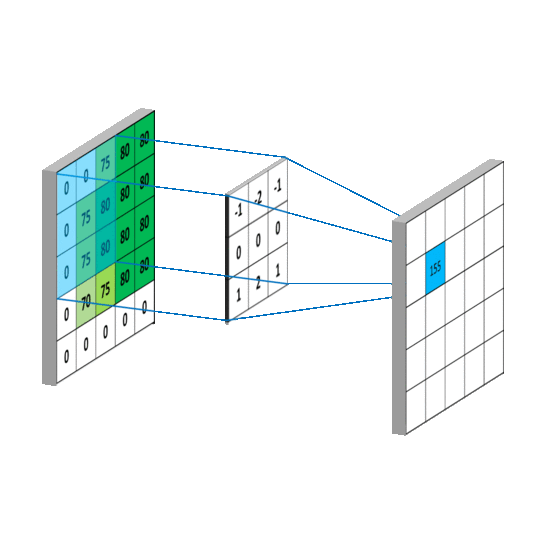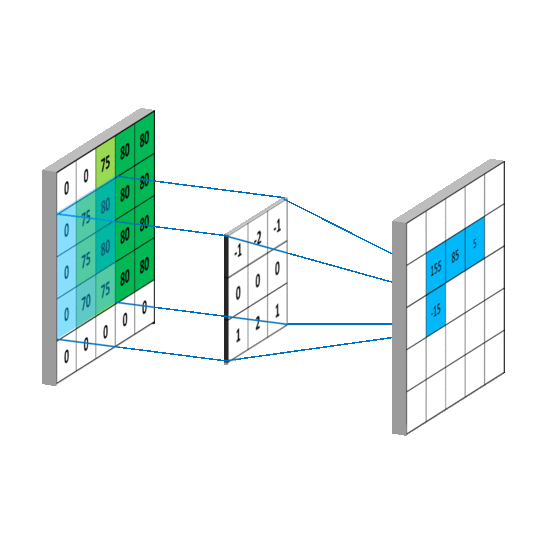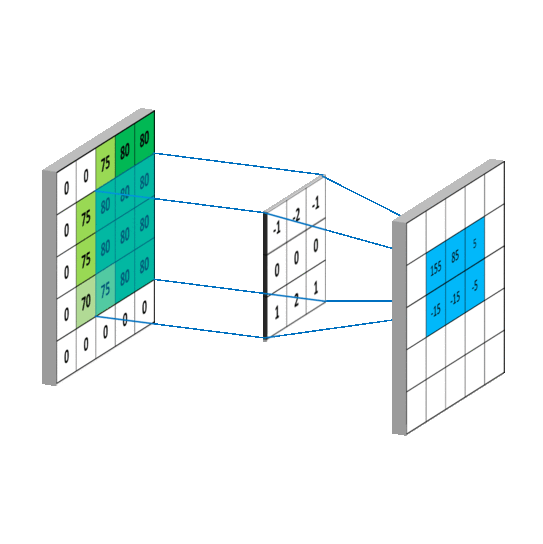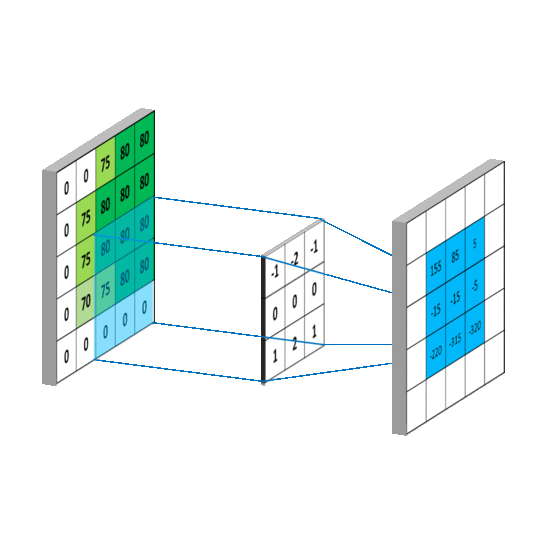

卷积与滤波

所谓滤波，就是消除不需要的频率成分,那么如何消除呢，我们知道傅里叶变换有个性质，时域卷积，频域相乘。
如图，图一和图二分别是f(t)和g(t)的频域图，图三是f(t)*g(t)的过程，频域相乘，得到图四的结果，这个例子相当于一个低通滤波器。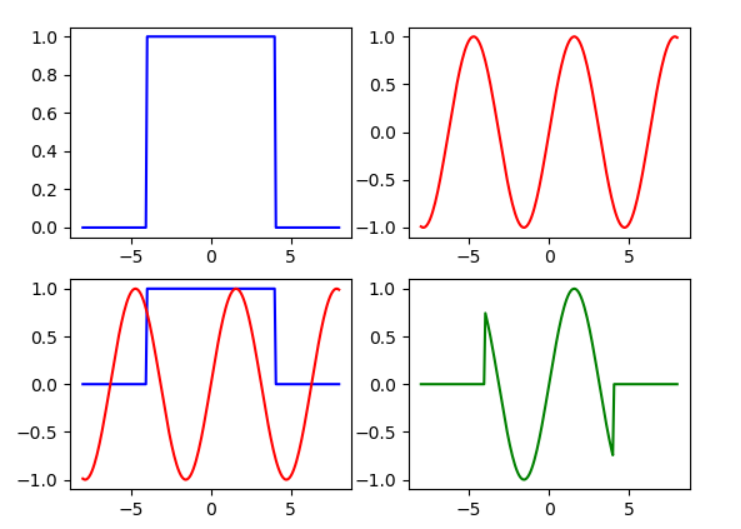

图像滤波

要解释图像的滤波，我们先要明白，图像在计算机里面表示是用二维矩阵的形式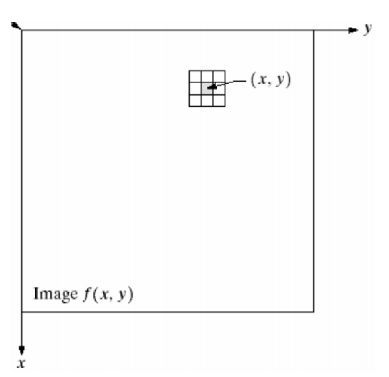

对应像素点的位置填充的数值为该点RGB的值，而RGB有三个值，所以呢我们就有三张图，称为通道。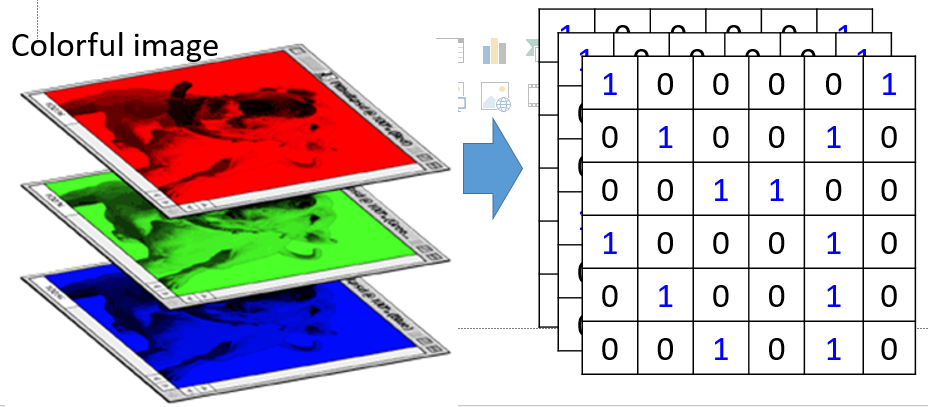

现在我们设计一个如下的滤波器，它能识别右边的曲线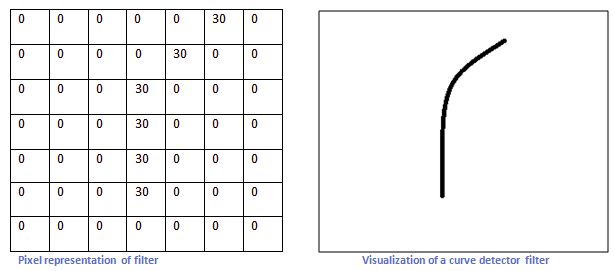

假设上面的核（滤波器）按照卷积顺序沿着下图移动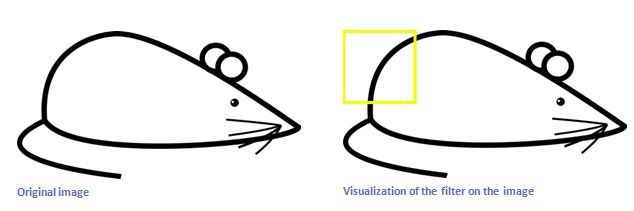

那么当它移动到上面的位置时，按照矩阵操作，将这个区域的图像像素值与滤波器相乘，我们得到一个很大的值（6600）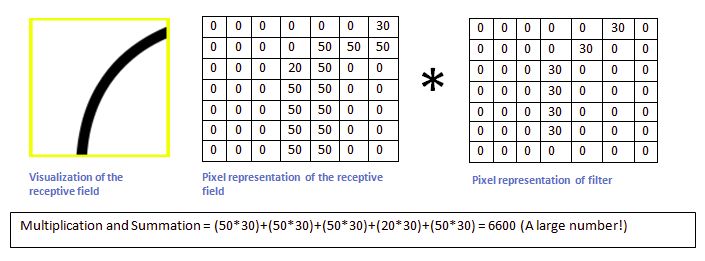

而当这个滤波器移动到其他区域时，我们得到一个相对很小的值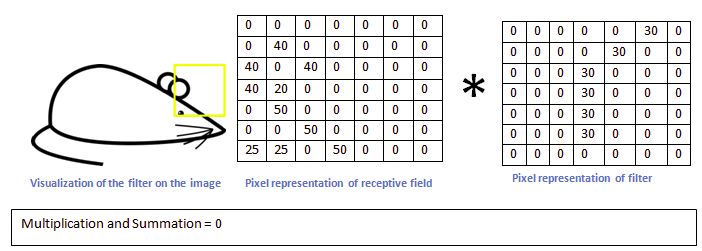

如此，我们就对原图进行了一次卷积，得到的结果中，在那个特定曲线和周边区域，值就很高，在其他区域，值相对低。这就是一张激活图。对应的高值区域就是我们所要检测曲线的位置。

小结

本文介绍的图像的卷积，在卷积神经网络中具有相当大的作用，用于图像特征的提取，我在后面对卷积神经网络也进行了详细的介绍。